グラフ見ただけでイヤ!⇒カンタンやん!?公立高校入試 数学のポイント
公立高校入試過去問研究!
今回は、苦手な人が多い一次関数の応用問題に挑戦したいと思います!
この記事の目次
1.例題 兵庫県公立高校入試過去問 引用
2.まずは、普通に解いてみます。
3.とにかくグラフだけを見る!
それでは例題から!

1.例題 兵庫県公立高校入試過去問 引用(改)
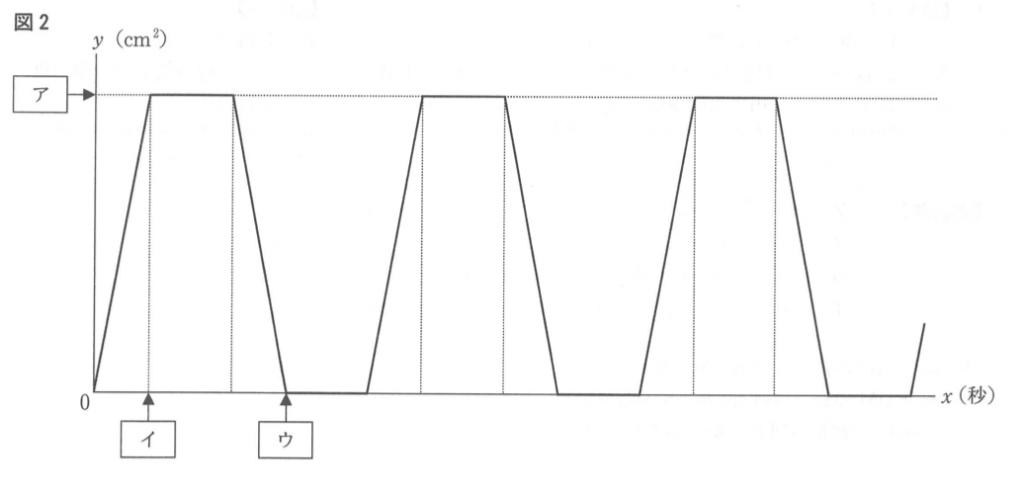
図1のようにAB=20cm、BC=30cmの平行四辺形ABCDがある。点Bから辺ADに垂線BHをひくとBH=16cmであった。
この平行四辺形の辺上を点Pは点Aを出発して、毎秒5cmの速さでA→B→C→D→A→…の順に動き、点Qは点Cを出発して、毎秒4cmの速さでC→D→A→B→C→…の順に動く。2点P,Qは、同時に出発するとして、次の問に答えなさい。
(1)図2は、2点が出発してからx秒後の⊿PADの面積をy平方センチメートルとしたときの、xとyの関係を表したグラフである。ア~ウにあてはまる数を求めなさい。
(2) 0≦ x ≦5のとき、2点が出発してからx秒後の△QADの面積をy平方センチメートルとするとき、yをxの式で表しなさい。
(3) △PADと△QADの面積が最初に等しくなるのは、2点が出発してから何秒後か、求めなさい。
(4) 2点が出発してから、はじめて点Pが点Qに追いつくまでに、△PADと△QADの面積が何秒か等しくなることが、数回ある。このうち最も長い時間△PADと△QADの面積が等しくなるのは、2点が出発してから何秒後から何秒後までか、求めなさい。
2.まずは、普通に解いてみます。
(1)アは点Pが点Bに重なるときなので、
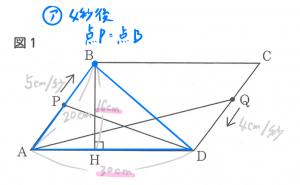
底辺30cm×高さ16cm×1/2 = 240・・・(ア)
点Pは毎秒5cm移動するので、各頂点の間を4秒→6秒→4秒→6秒…と移動。
(ⅰ)のとき、点Pが点Bの位置に来るので、4(秒後)・・・(イ)
(ⅲ)のとき、点Pが点Dの位置に来るので、14(秒後)・・・(ウ)
(2)△QADの底辺30cmで高さが…xで表したいけど…あれ?
この後さらに複雑になり、教科書・定期テストのレベルではなかなか対処が難しくなります!
どう考えていけばいいの?

そんな時は、
3.とにかくグラフだけを見る!
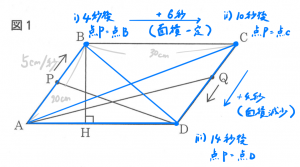
まずグラフを完成させます!
△PAD、△QADのグラフをどちらも先に書き込んでしまいます!
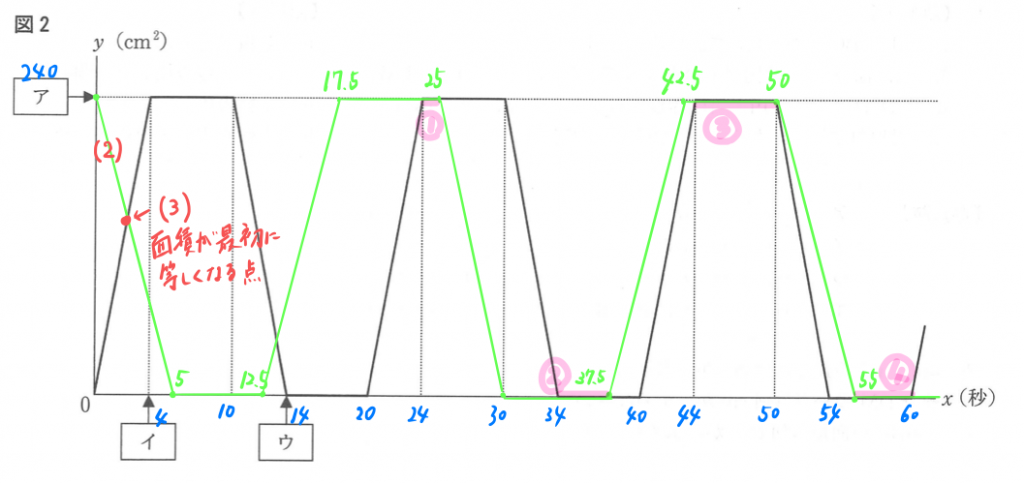
何秒後かも書き込んでおきました。
△PADは、毎秒4cm動くので、4秒→6秒→4秒→6秒と移動していき、
△QADは、毎秒5cm動くので、5秒→7.5秒→5秒→7.5秒と移動します。
それでは先程の続きで(2)から、
傾き -240/5=-48、切片240より、y=-48x+240・・・(2答え)
(3)初めて△PADと△QADの面積が等しくなるのは、図の2つの直線の交点をのところです!
y=-48x+240
y=60x
の連立方程式を解いてx=20/9(計算省略しました。)
20/9・・・(3答え)
(4)も長い時間△PADと△QADの面積が等しくなるのは、
図2の蛍光ピンク③のところです!
44秒後から50秒後まで・・・(4答え)
Beautiful Mathematics!
文章題というよりは、とにかくグラフとして捉えること!
※こういう1次関数のグラフは交通機関の運行計画を作成する際によく利用されています。(ダイヤグラムと呼ばれています。)ほぼ毎年出題される超頻出問題!がんばろう!
楽しい!もっと数学を勉強したい!という人は是非、中谷塾へ♪